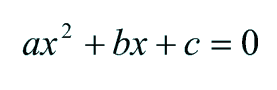
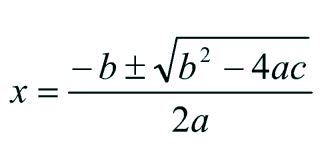
| the quadratic equation
|
the solution for the two roots as
given by most texts.
|
however, the standard formula isnt the best way to calculate the roots because its numerically unstable. lets make a test suite of 6 cases (taken from the hp-15c advanced function handbook p207).
| a | b | c | x1 (rounded to 10 figs) | x2 (rounded to 10 figs) | |
| 1 | 1 | -4 | 3 | 1 | 3 |
| 2 | 1 | 0 | 4 | 2i | -2i |
| 3 | 10^-13 | -2 | 1 | 2*10^13 | -0.5 |
| 4 | 654323 | -1308644 | 654321 | 1 | 0.9999969434 |
| 5 | 11713 | -1470492 | 46152709 | 62.77179203+/- i8.537522411*10^-5 | |
| 6 | 80841 | -1975288 | 12066163 | 12.21711755+/- i*1.374513618*10^-3 | |
let see what we get out of some calculators that claim to solve the quadratic
| model | # | x1 | x2 | score |
| casio fx-5500l | 1 | 3 | 1 | yes |
| 2 | 2i | -2i | yes | |
| 3 | 2*10^13 | 0 | no | |
| 4 | 0.9999984717 | double root | no | |
| 5 | 62.77179203 | double root | no | |
| 6 | 12.21711755+/-i*1.374541449*10^-3 | 1/2 (inaccurate) | ||
| score | 42% | |||
| sharp el-9900 | 1 | 3 | 1 | yes |
| 2 | 2i | -2i | yes | |
| 3 | 2*10^13 | 0 | no | |
| 4 | 1 | 0.999996943 | yes | |
| 5 | 62.77179203 +/i i*0.000085375 | 1/2 (inaccurate) | ||
| 6 | 12.21711755 +/- i*0.001374513 | yes | ||
| score | 75% | |||
the sharp does quite well, largely due to its internal precision, but the casio fares poorly, case 4 is not a double root and case 5 is not-real, even the 9900 gets case 3 wrong missing the root x near 0.5 completely.